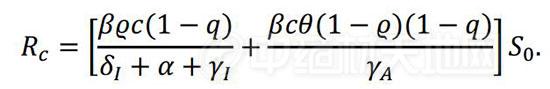下拉刷新
加载中...
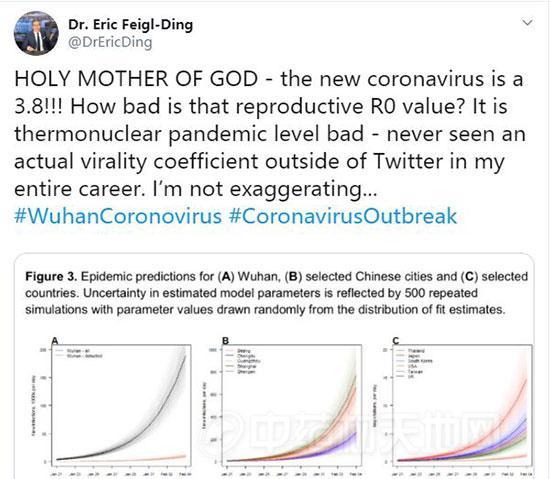
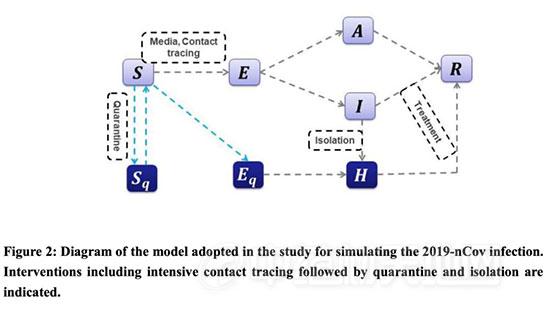
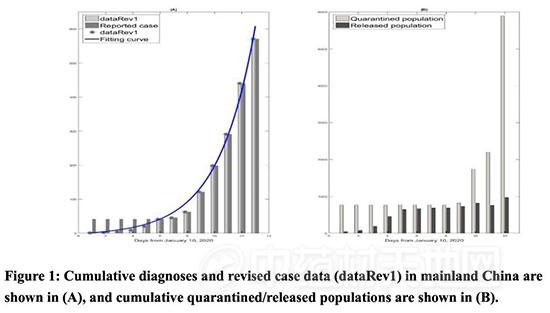
新型冠状病毒传染性有多强?何时达到峰值?来看一下数学和统计建模结果
2020-01-30 08:21:28
推荐资讯
-
产业观察 黄璐琦院士建议:尽早使用中成药对医学观察期人员进行分层干预2020-01-30 08:07

-
产业观察
专家:光滑的地方病毒更易存活 衣物上存活时间短
2020-01-30 08:02
-
产业观察 澳大利亚成功培育新型冠状病毒毒株,有助疫苗研制2020-01-29 21:54

-
产业观察
好消息!中科院武汉病毒所筛出能较好抑制新型冠状病毒药物
2020-01-29 21:32
-
产业观察
确诊人数超过"非典" 专家:无须对病例数过于恐慌
2020-01-29 20:29
热门资讯
-
产业观察
专题文章 | 黄河流域中药资源现状与产业高质量发展建议
2026-02-12 13:30
-
产业观察 2025年中药类商品进出口分析2026-02-12 11:21

-
产业观察
以“质”为犁 深耕中药材种植希望的田野
2026-02-12 11:49
-
产业观察
新春走基层|中医药文化添彩年货集市
2026-02-12 10:56
-
产业观察 富兴镇:丹参红了,中药材种出“甜日子”2026-02-12 10:21

-
产业观察 土里掘“金”,小药材种出大希望2026-02-12 10:31

上拉刷新
加载中...
正在加载